"Gimbal lock"
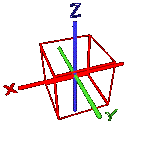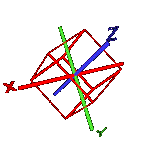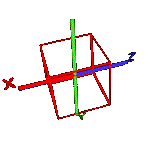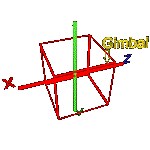
Sweep pointer in the centre.
Rotate cube on 90 degrees around axis
Y.
Now rotate cube around axis X. The corner Y not change.
You see,
presently cube revolves is CORRECT!
Now once again sweep the pointer in the centre.
Rotate cube on 90
degrees around axis X.
Now rotate cube around axis Y. The corner X not
change.
You see, presently cube revolves is NOT CORRECT!
The cube begins
to revolve not around axis Y, but around axis Z!!
This problem of the Eyler equations. The problem possible to solve at
quaterni.
But as this do in programming?
"Шарнирный замок"
"Шарнирный замок" - это название проблемы, возникающей при использовании
Эйлеровых углов. Из-за того, что конечный результат серии вращений зависит от
порядка промежуточных вращений, иногда случается, что вращение вокруг одной оси
отображается на вращение вокруг другой оси. Даже хуже, может быть невозможно
вращать объект вокруг желаемой оси. Вот это и есть "Шарнирный замок". Например,
предположим, что объект последовательно вращают вокруг Z (на небольшой угол), Y,
X - осей, и угол вращения вокруг оси Y равен 90 градусам. В этом случае вращение
вокруг оси Z происходит первым и, поэтому, корректно. Вращение вокруг оси Y тоже
совершается корректно. Однако после вращения вокруг оси Y на 90 градусов, ось X
отображается на ось Z. Таким образом, совершая вращение вокруг (относительной)
X-оси мы фактически вращаем объект вокруг (абсолютной) оси Z. Единственное
решение этой проблемы - использование кватернионов.

== Описание ==
"Шарнирный замок" - это название проблемы, возникающей при использовании Эйлеровых углов.
Из-за того, что конечный результат серии вращений зависит от порядка промежуточных вращений,
иногда случается, что вращение вокруг одной оси отображается на вращение вокруг другой оси.
Когда оси двух шарниров оказываются параллельными друг другу, вы теряете одну степень свободы
в этой системе. В этом случае может быть невозможно вращать объект вокруг желаемой оси.
== Пример ==
Предположим, что объект последовательно вращают вокруг Z (на небольшой угол), Y, X - осей,
и угол вращения вокруг оси Y равен 90 градусам. В этом случае вращение вокруг оси Z
происходит первым и, поэтому, корректно. Вращение вокруг оси Y тоже совершается корректно.
Однако после вращения вокруг оси Y на 90 градусов, ось X отображается на ось Z.
Таким образом, совершая вращение вокруг (относительной) X-оси мы фактически вращаем объект
вокруг (абсолютной) оси Z.
== Решение проблемы ==
Задача решается средствами векторной алгебры, в случае полного определения траектории вращения каждой из точек 3D объекта. Далее перемещение точки вычисляется в афинной системе координат. Все плоскости вращения удерживаются единым вектором нормали. Такой алгоритм обеспечивает корректный пересчёт углов вращения (собственного вращения, прецессии и нутации) и позволяет избежать "шарнирного замка", возникающего при использовании эйлеровых углов в классической 3D матрице вращения. Тем самым отменяется необходимость в использовании кватернионов при построении 3D сцены кругового движения и круговом обзоре трёхмерного объекта.
Полное же решение проблемы возможно при использовании кватернионов. В ориентации кватерниона используются комплексные числа. Ориентация кватерниона представляется тремя осями поворота (x,y,z) и углом поворота (w). Кватернион обеспечивает кратчайший, наиболее эффективный контур вращения. Он также позволяет выполнять сглаживание без эффекта «шарнирного замка». Блокировка вращения может произойти, когда во время вращения вокруг двух или более осей оси оказываются расположенными параллельно друг другу, что приводит к получению непредвиденных результатов.
== Ссылки ==
[http://avs.chat.ru/gimballock.htm] Advanced Visualisation Studio
[http://avs.chat.ru/sphere3d.htm] 3D Circle calculation
== См. также ==
[[Матрицы вращения]]
Матрица вращения употребляется для вращения набора точек в пределах координатной системы.
В то время, как каждая точка получает новые координаты, относительные расстояния между ними
не меняются. Все вращения определяются с помощью тригонометрических функций - синусов и косинусов.
[[Эйлеровы углы вращения]]
Эйлеровыми углами называют углы, определяющие положение прямоугольной декартовой
системы координат относительно другой прямоугольной декартовой системы координат
с тем же началом координат и с той же ориентацией. Угол собственного вращения - вокруг оси OZ,
угол прецессии - вокруг оси OZ1, угол нутации - вокруг линии узлов ОК.
http://avs.chat.ru/sphere3d.htm
http://ru.vlab.wikia.com/wiki/Шарнирный_замок
http://ru.science.wikia.com/wiki/Шарнирный_замок
http://www.wikiznanie.ru/ru-wz/index.php/Шарнирный_замок
http://avs.chat.ru
