English ^ Русский
index
А.Панов АЛГОРИТМ НОРМАЛИЗОВАННОГО 3D ПОВОРОТА
(ВЫЧИСЛЕНИЕ ОКРУЖНОСТИ в 3D системе координат)
Цель: Построение модели 3D сцены для кругового
обзора.
Задача: Вычисление окружности, которая образуется
пересечением произвольной плоскости со сферой.
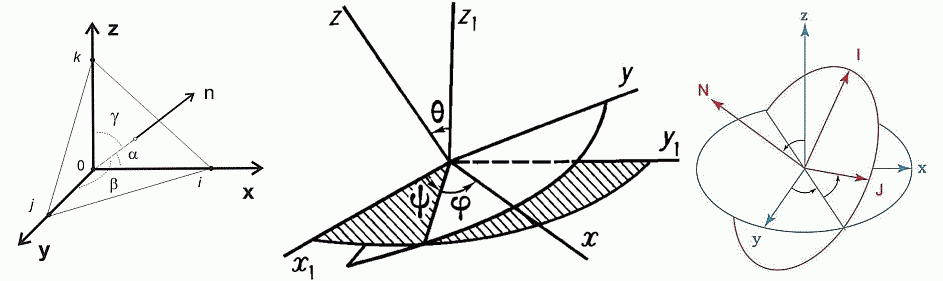
По заданному вектору перемещаемой точки P(xp,yp,zp) вычисляется радиус
опорной сферы rp и параметр секущей плоскости pc от заданного вектора нормали
N(xn,yn,zn). "Неопределённость" может возникнуть, если вектор нормали имеет
нулевое значение (nr=0), поэтому хотя бы одна из составляющих вектора нормали
всегда должна оставаться не равной нулю. Затем вычисляется радиус секущей
окружности rc и координаты её центра R(xr,yr,zr). Исходная точка для отсчёта
начала движения задаётся по окружности вектором P(xp-xr,yp-yr,zp-zr). Здесь
phi=php является полярной координатой точки объекта на рассчётной траектории до
начала поворота, а phi=php+dph полярной координатой после завершения поворота.
При просчёте траектории поворота, dph последовательно принимает все значения от
0 до 2*pi для одной указанной точки (xp,yp,zp), а при вычислении поворота всего
объекта, все точки (x,y,z) пересчитываются с одним заданным углом поворота
dph.
Ось абсцисс аффинной системы координат (phi=0) задаётся вектором
I(xi-xr,yi-yr,zi-zr). Скалярное произведение двух радиус-векторов P,I, и
смешанное произведение трех векторов I,N,P позволяет определить php полностью.
Векторное произведение векторов I,N даёт направление аффинной оси ординат -
вектор J(xj,yj,zj). Скалярное произведение векторов P,J определяет проекцию
рассчётного вектора P на аффинную ось ординат. Линейно независимые вектора I,J,N
задают ортонормированный базис. В процессе вычислений может происходить деление
на ноль, когда нулю равен радиус секущей окружности (rc=0). Практически это
означает, что точка объекта находится непосредственно на оси вращения, и поэтому
не перемещается в пространстве. Такие точки необходимо исключать из пересчёта
вращения. При вычислении вращения конкретного 3D объекта, траектории вычисляются
отдельно для его каждой узловой точки. Все плоскости вращения удерживаются
единым вектором нормали, который и является осью поворота объекта или осью
собственного вращения, если ось проходит через центр масс.
Корректное решение задачи из
серии three-stage gyro (трехстепенный гироскоп) при использовании
кватернионов и эйлеровых углов классической 3D матрицы вращения в
принципе невозможно.
Алгоритм обеспечивает корректный пересчёт углов вращения (собственного
вращения, прецессии и нутации) и позволяет избежать "шарнирного замка",
возникающего при использовании эйлеровых углов в классической 3D матрице
вращения. Тем самым отменяется необходимость в использовании кватернионов при
построении 3D сцены кругового движения и круговом обзоре трёхмерного объекта.
Алгоритм нормализованного 3D поворота позволяет корректно решать задачи из серии
three-stage gyro (трехстепенный гироскоп), которые решить при использовании 3D
матрицы вращения в принципе невозможно, и в которых даже при использовании
кватернионов может возникать блокировка вращения, когда во время поворота вокруг
двух или более осей, оси оказываются расположенными параллельно друг другу, что
приводит к получению непредвиденных результатов.
входящие : xn,yn,zn, xp,yp,zp, dph
переменные :
rp,rj,rc,pc,mu, nx,ny,nz,nr, xr,yr,zr, xi,yi,zi, xj,yj,zj, ip,jp, theta,psi,
phi,php
выходящие : x,y,z
Сфера (0,0,0)
x^2 + y^2 + z^2 =
rp^2
Определение секущей плоскости по точке на плоскости и вектору
нормали
xn*(x-xp) + yn*(y-zp) + zn*(z-zp) = 0
Общее (полное)
уравнение плоскости
xn*x + yn*y + zn*z + ( - xn*xp - yn*zp - zn*zp) =
0
Нормированное уравнение секущей плоскости
x*cos(oxn) +
y*cos(oyn) + z*cos(ozn) - рc = 0
Направляющие косинусы
nx =
cos(oxn); ny = cos(oyn); nz = cos(ozn);
Единичный нормальный вектор
секущей плоскости
nx^2 + ny^2 + nz^2 = 1
Точка перемещается
по секущей окружности
rp^2 = rc^2 + pc^2
Скалярное произведение векторов P(xp-xr,yp-yr,zp-zr) и
I(xi-xr,yi-yr,zi-zr)
rc^2 * cos(fp) = (xp-xr)*(xi-xr) +
(yp-yr)*(yi-yr) + (zp-zr)*(zi-zr)
ip = rc * cos(fp)
Смешанное произведение трех векторов
Векторное произведение
I(xi-xr,yi-yr,zi-zr) и N(xn,yn,zn)
xj=(yi-yr)*zn-(zi-zr)*yn;
yj=(zi-zr)*xn-(xi-xr)*zn; zj=(xi-xr)*yn-(yi-yr)*xn;
rj=sqrt(xj*xj+yj*yj+zj*zj);
Скалярное произведение
P(xp-xr,yp-yr,zp-zr) и J(xj,yj,zj)
rc*rj*cos(pi/2-fp) =
(xp-xr)*xj + (yp-yr)*yj + (zp-zr)*zj
jp = rc *
cos(pi/2-php)
Вращение точки вокруг оси вектора нормали ON
phi=i*2*pi;
x1=r*cos(phi); y1=r*sin(phi); z1=0;
Матрица вращения вокруг оси
OY
x2=x1*cos(theta)-z1*sin(theta);
z2=x1*sin(theta)+z1*cos(theta);
y2=y1;
Матрица вращения
вокруг оси OZ
x3=xr+x2*cos(psi)-y2*sin(psi);
y3=yr+x2*sin(psi)+y2*cos(psi);
z3=zr+z2;
*
// Сфера проходит через точку (xp,yp,zp) //
rp=
sqrt(xp*xp+yp*yp+zp*zp);
// Нормирующий множитель //
mu = 1/sqrt(xn*xn+yn*yn+zn*zn);
// Единичный
нормальный вектор секущей плоскости //
nx = xn*mu; ny = yn*mu; nz =
zn*mu;
nr = sqrt(nx*nx + ny*ny + nz*nz); // nr=1 (!)
// Расстояние до секущей плоскости //
pc = xp*nx + yp*ny
+ zp*nz;
// Центр секущей окружности //
xr = pc*nx;
yr = pc*ny; zr = pc*nz;
// Радиус секущей окружности
//
rc = sqrt(rp*rp - pc*pc);
// Угол вектора
нормали от оси OZ (ozn) //
theta = - acos(nz);
//
Угол проекции нормали от оси OX //
psi =
atan2(ny,nx);
// Вычисление аффинной оси абсцисс phi=0
//
xi=xr+rc*cos(psi)*cos(theta); yi=yr+rc*sin(psi)*cos(theta);
zi=zr+rc*sin(theta);
// Скалярное произведение
//
ip =
((xp-xr)*(xi-xr)+(yp-yr)*(yi-yr)+(zp-zr)*(zi-zr))/rc;
// Смешанное
произведение //
xj =(yi-yr)*zn-(zi-zr)*yn;
yj=(zi-zr)*xn-(xi-xr)*zn; zj=(xi-xr)*yn-(yi-yr)*xn;
rj =
sqrt(xj*xj+yj*yj+zj*zj);
// Вычисление аффинной оси ординат phi=pi/2
//
jp = ((xp-xr)*xj + (yp-yr)*yj + (zp-zr)*zj)/rj;
php = -
atan2(jp,ip); php = if( below(rc,0.001),0,php ); // rc|=0 (!)
phi=php+i*2*pi;
// Вычисление поворота
//
x=xr+rc*(cos(phi)*cos(psi)*cos(theta)-sin(phi)*sin(psi));
y=yr+rc*(cos(phi)*sin(psi)*cos(theta)+sin(phi)*cos(psi));
z=zr+rc*(cos(phi)*sin(theta));
*
Разработка алгоритма: А.Панов
Способ построения 3-D сцены кругового движения
English ^ Русский
index
A.Panov REAL 3D ROTATION ALGORITHM
(3D
CIRCLE calculation)
The Purpose: Build 3D scene models for circular
review.
The Problem: Calculation of circumferences, which is
formed by crossing of free plane with sphere.
Are they first calculate parameters of the sphere and normal vector of
crossing planes. After calculate radius of crossing circumferences and
coordinates of her centre. This algorithm ensures the correct recalculation an
rotations angles and allows to avoid "lock", appearing when use euler angles in
classical 3D rotation matrix. Hereunder need is cancealled to use a quaternions.
This means the new way of the building 3D scene of the circular motion and
possibility of the circular review of any three-dimensional object on planes
(three-degree gyroscopes). The distance prior to plane of the rotation is fixed
along coordinate of the point, across which passes the secant plane. The
rotation trajectory is fixed for each 3D object point to uniform normals
vector.
gyroscopes.avs
Correct decision of the three-stage
gyro task by means of euler angles in classical 3D rotation matrix and
quaternions impossible in principle.
http://avs.chat.ru/sphere3d.htm#en .. avs.chat.ru/sphere3d.htm
http://avs.chat.ru/sphere3d.avs .. avs.chat.ru/sphere3d.avs
input : xn,yn,zn, xp,yp,zp, dph
used : rj,rc,pc,mu,
nx,ny,nz, xr,yr,zr, xi,yi,zi, xj,yj,zj, ip,jp, theta,psi,
phi,php
output : x,y,z
km=1; kd=0/33; pi=$PI; piw=2*$PI; deg=180/$PI;
xn=getkbmouse(2)*km;
yn=-getkbmouse(1)*km; // xn=0.6; yn=0.6; zn=0.6;
zn=if(
above((xn*xn+yn*yn),1), 0, sqrt(1-(xn*xn+yn*yn)) );
x=-0.5; y=-0.5; z=-0.5; // rp=0.87;
xp=x; yp=y; zp=z;
// CROSSING PLANE CALCULATION //
mu =
1/sqrt(xn*xn+yn*yn+zn*zn);
nx = xn*mu; ny = yn*mu; nz =
zn*mu;
pc = xp*nx + yp*ny + zp*nz;
xr = pc*nx; yr = pc*ny; zr
= pc*nz;
rc = sqrt((xp*xp+yp*yp+zp*zp) - pc*pc);
theta = - acos(nz);
psi = atan2(ny,nx);
// (1) INPUT POINT (phi=php) CALCULATION // rc|=0 (!)
xi=xr+rc*cos(psi)*cos(theta); yi=yr+rc*sin(psi)*cos(theta);
zi=zr+rc*sin(theta);
ip =
((xp-xr)*(xi-xr)+(yp-yr)*(yi-yr)+(zp-zr)*(zi-zr))/rc;
xj =
(yi-yr)*zn-(zi-zr)*yn; yj=(zi-zr)*xn-(xi-xr)*zn;
zj=(xi-xr)*yn-(yi-yr)*xn;
rj = sqrt(xj*xj+yj*yj+zj*zj);
jp =
((xp-xr)*xj + (yp-yr)*yj + (zp-zr)*zj)/rj;
php = - atan2(jp,ip); php = if(
below(rc,0.001),0,php );
// (2) INPUT POINT (phi=php) ITERATION //
k=0;
loop(360,
assign(phi,k*2*pi/360)+
assign(x,
xr+rc*(cos(phi)*cos(psi)*cos(theta)-sin(phi)*sin(psi)) )+
assign(y,
yr+rc*(cos(phi)*sin(psi)*cos(theta)+sin(phi)*cos(psi)) )+
assign(php, if(
band(below(abs(x-xp),0.009),below(abs(y-yp),0.009)) , phi , php)
)+
assign(k,k+1) );
phi=php+dph; // phi=php+i*2*pi;
reg00= php*deg;
reg04= psi*deg; reg05= theta*deg;
reg08= rc; reg09= pc;
reg01= xn; reg02= yn; reg03=
zn;
reg11= xi-xr; reg12= yi-yr; reg13= zi-xr;
reg21= xj; reg22= yj; reg23=
zj; reg24= rj;
reg31= xr; reg32= yr; reg33= zr;
// TUMBLING CALCULATION
//
x=xr+rc*(cos(phi)*cos(psi)*cos(theta)-sin(phi)*sin(psi));
y=yr+rc*(cos(phi)*sin(psi)*cos(theta)+sin(phi)*cos(psi));
z=zr+rc*(cos(phi)*sin(theta));
*
